Con una breve nota histórica como introducción, construiremos la función “sombrero mexicano” conmemorando el movimiento de la Revolución Mexicana.

La Revolución Mexicana (1910-1917) fue un evento importante en la historia de México. Surgió por las difíciles condiciones económicas y sociales en las que se encontraba la población mexicana a causa de la dictadura de Porfirio Díaz.

En 1910, después de 35 años de dictadura, Porfirio Díaz fue reelecto para un nuevo periodo presidencial (1910-1914). Este acontecimiento provocó un descontento generalizado en todo el país y los mexicanos tomaron las armas para acabar con la dictadura de Díaz. Se considera que la Revolución Mexicana finalizó con la promulgación de la Constitución Política de los Estados Unidos Mexicanos de 1917.

En la actualidad, en México, el 20 de noviembre se conmemora el inicio de la Revolución Mexicana. En este día se realizan distintos eventos que incluyen un desfile militar-deportivo así como presentaciones artísticas de danza y música en todo el país.

Como parte de los eventos de conmemoración del 20 de noviembre, se suelen hacer representaciones de vestimenta típica de los tiempos de la revolución. El “sombrero mexicano” es muy característico y uno de los accesorios más reconocidos en todo el mundo.

El sombrero mexicano no ha pasado desapercibido en la comunidad de matemáticos. La función “sombrero mexicano” (mexican hat, en inglés) es una función que debe su nombre a la peculiar forma que evoca el accesorio típico de la vestimenta mexicana en tiempos de la revolución.

En esta página, daremos una definición corta de la función “sombrero mexicano” y mostraremos cómo construirla usando MATLAB/Octave. Con esta breve nota histórica y la construcción de la función “sombrero mexicano,” conmemoramos con el lector el movimiento de la Revolución Mexicana.

En matemáticas, existe cierto tipo de funciones conocidas como onduletas (wavelets, en inglés). A grandes rasgos, podemos decir que las onduletas son funciones oscilatorias de duración finita. En el campo del análisis numérico, los matemáticos han estudiado exhaustivamente las onduletas debido a sus aplicaciones prácticas. Por ejemplo, las onduletas se han aplicado con éxito para la compresión de datos, extracción de características en señales sísmicas, y filtros para procesamiento de datos.

En esta página analizaremos brevemente la onduleta de Ricker, también conocida como función “sombrero mexicano.”

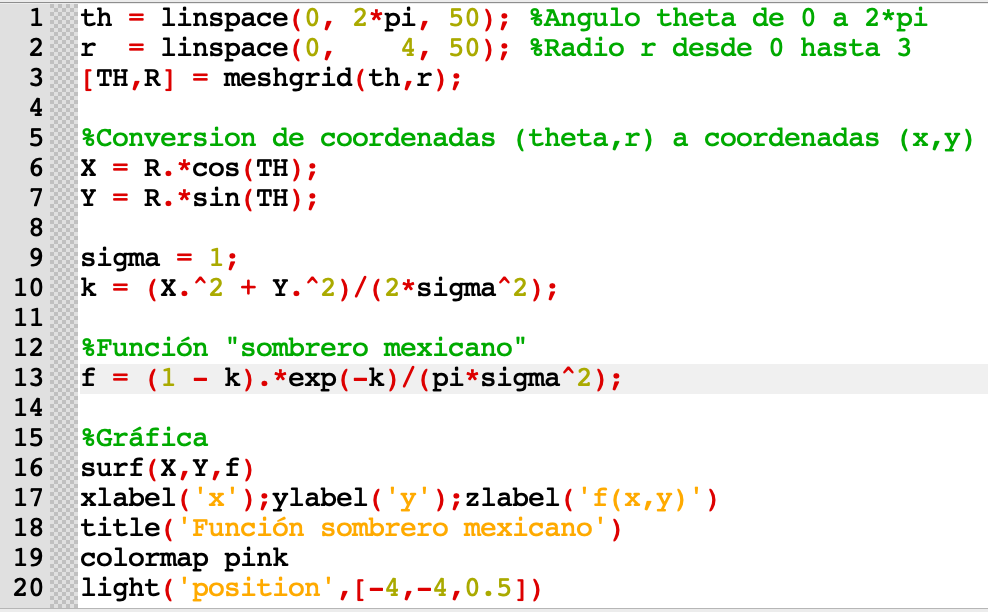
La función sombrero mexicano es proporcional a la segunda derivada de una función gaussiana. Específicamente, para dos dimensiones, la función sombrero mexicano se define como en la ecuación (1).

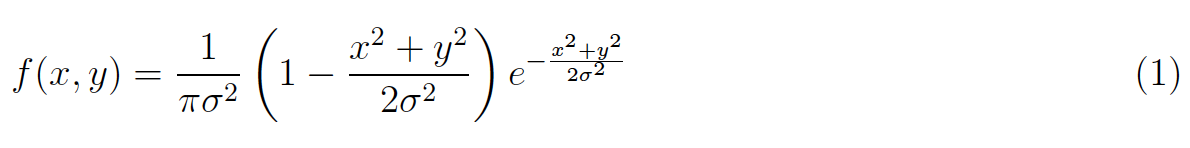
La figura 4 proporciona el código en MATLAB/Octave para construir una gráfica de esta función. Observe que para construir la función se generaron los puntos (x,y) a partir partiendo de coordenadas cilíndricas (θ, r). Esta elección de coordenadas nos permite realizar una gráfica resaltando la simetría (de revolución) de la función.

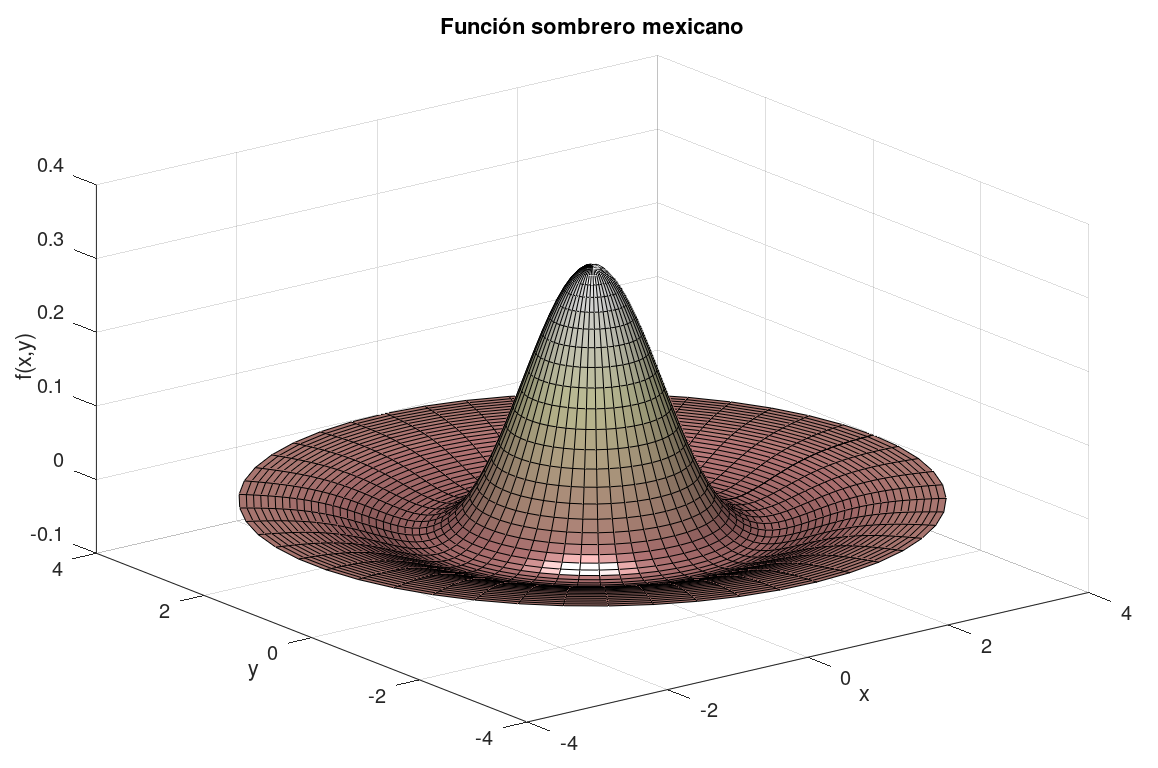
Finalmente, la figura 5 muestra el resultado al ejecutar el código proporcionado (Se usó GNU Octave Versión 5.1.0, 2019). Esta función permite ilustrar conceptos tales como coordenadas cilíndricas, transformación de coordenadas, y simetría.

Esperamos que esta página haya sido de tu interés y despierte la curiosidad para buscar respuestas a preguntas de investigación. Por ejemplo,

• ¿Qué otras onduletas existen?,
• ¿Cuáles son las ventajas y desventajas que presenta cada una de ellas?,
• ¿Cómo se usan en la práctica; por ejemplo, para filtrar una imagen contaminada por ruido aleatorio?, y
• ¿Qué es la transformada wavelet?

Cerramos esta página conmemorando a los mexicanos que hace 109 años iniciaron el movimiento que nos legó un México mejor.